Neural Architecture Search

Primitive Operations

• Linear: in_channels = 8, out_channels = 16
• Normal Convolution: in_channels = 8, out_channels = 16, groups=1
  • One convolution over all input channels producing all output channels.
  • Input: CxHxW, Filter: FxCxKxK, Output: FxHxW
  • F Filters of size CxKxK
• Depth-Wise Convolution: in_channels = 8, out_channels = 8, groups=8
  • Eight independent convolutions, each over one input channel producing one output channel.
  • Input: CxHxW, Filter: Cx1xKxK, Output: CxHxW
  • C Filters of size 1xKxK
  • Each filter is applied only to its corresponding input channel, producing an output for each channel separately.
• Grouped Convolution: in_channels = 8, out_channels = 16, groups=4
  • Four independent convolutions, each over 2 input channels (in_channels/groups) producing 4 output channels (out_channels/groups).
  • Input: CxHxW, Filter: F/G x C/G x KxK, Output: FxHxW
  • G groups of F/G filters of size C/G x KxK.
  • if groups == in_channels becomes Depth wise convolution
• Point-Wise Convolution (1x1 Convolution): in_channels = 8, out_channels = 16, groups=1
  • Each filter performs a linear combination across the depth channels, effectively transforming the depth without changing the spatial dimensions.
  • Input: CxHxW, Filter: FxCx1x1, Output: FxHxW
  • F Filters of size 1xKxK

Classical Building Blocks

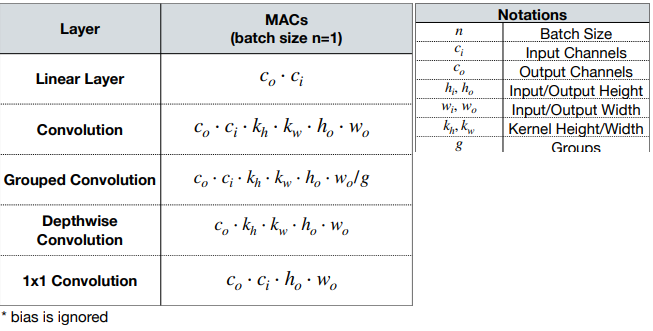
ResNet: Bottleneck block

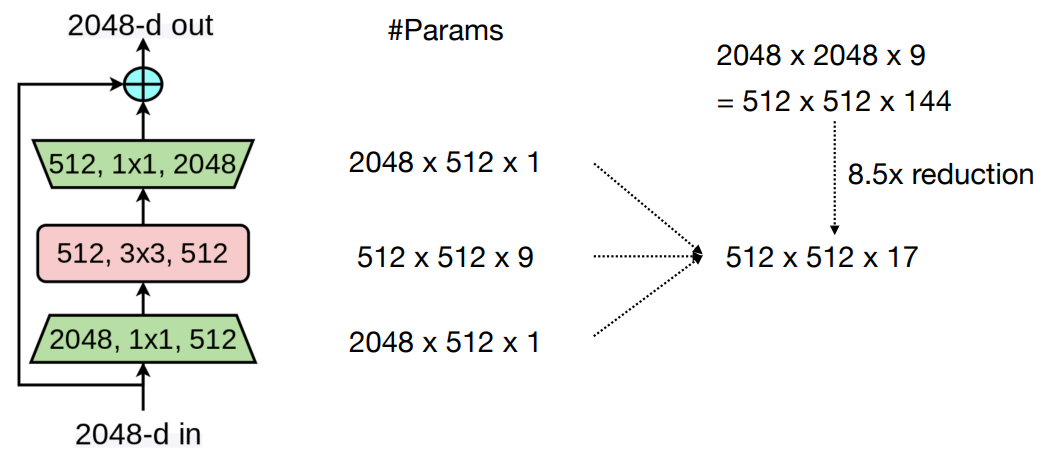
ResNeXt: Grouped Convolution

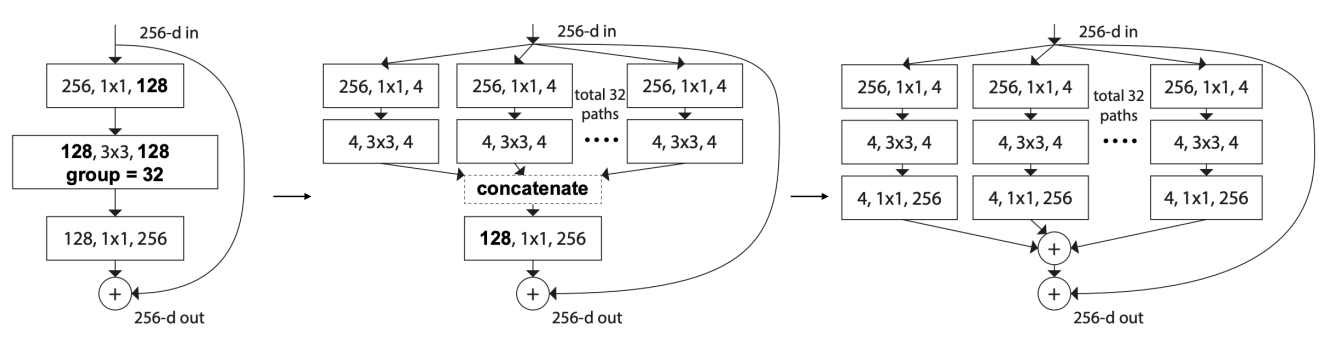
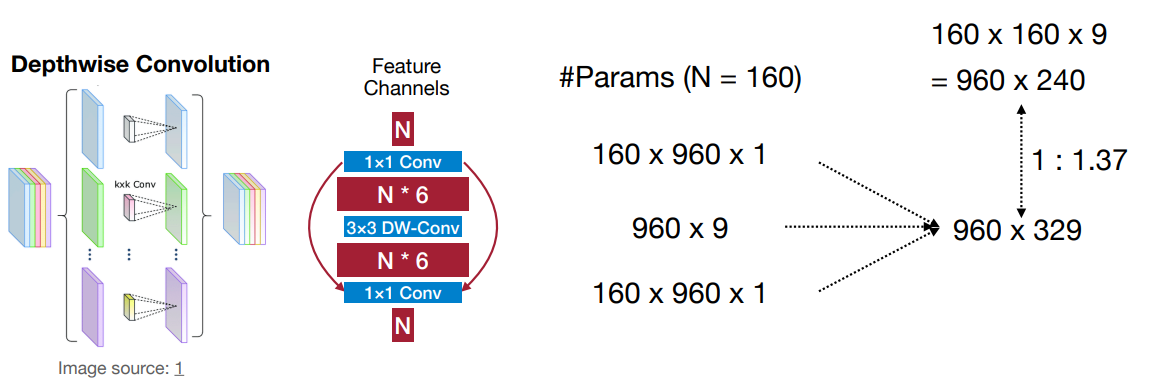
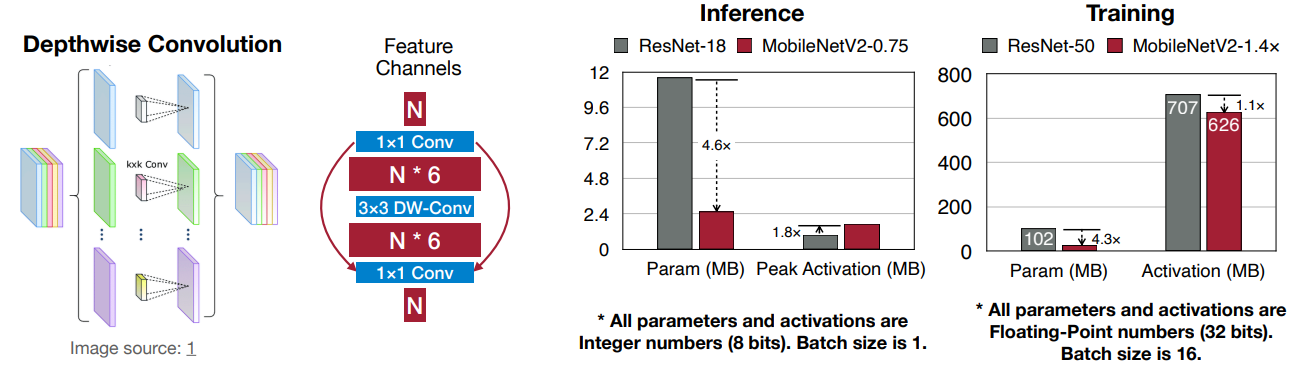
MobileNet: Depthwise Convolutions

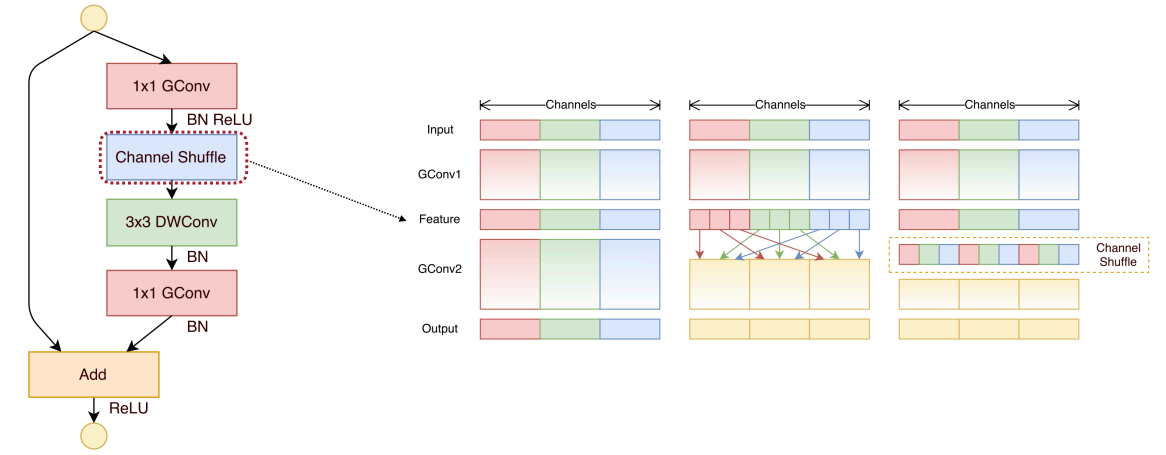
ShuffleNet: 1x1 Group Conv & Channel shuffle

• Further reduce the cost by replacing 1x1 convolution with 1x1 group convolution.
• Exchange information across different groups via channel shuffle

NAS

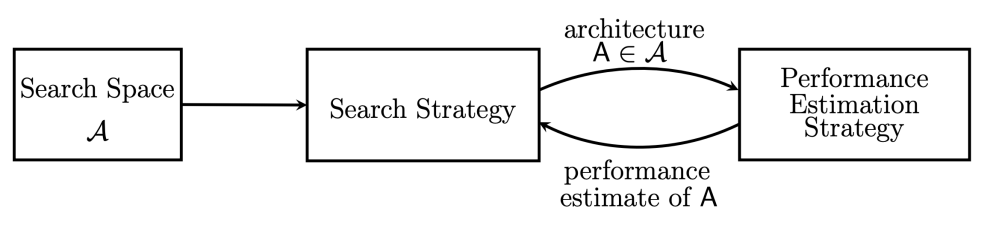
Search Space

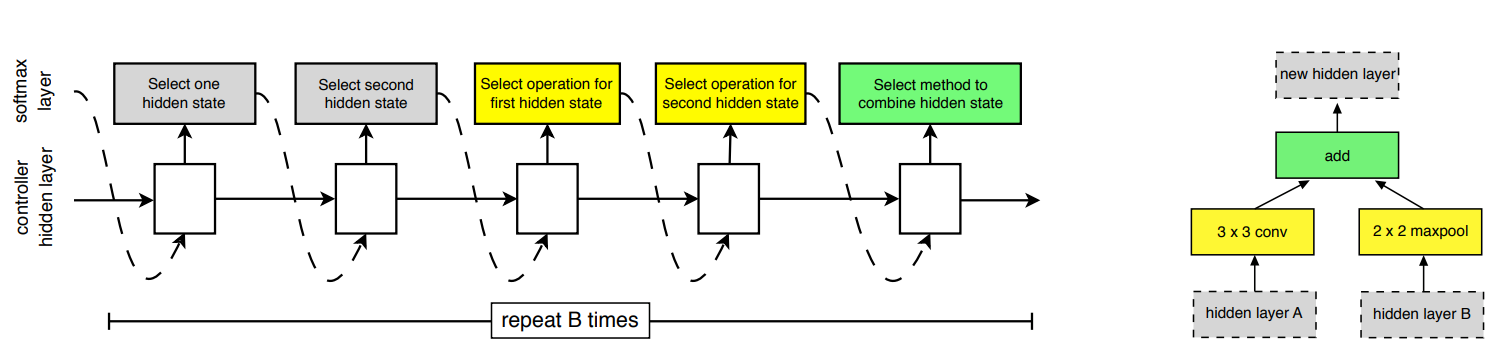
Cell-level Search Space

For i in range(1, B+1):

1. Identify the first input.
2. Identify the second input.
3. Select the transformation operation for the first input.
4. Select the transformation operation for the second input.
5. Choose the method to combine the results from the two transformed inputs. Result:
   • A cell generated after one step

Size of search space: Question: Assuming that we have two candidate inputs, M candidate operations to transform the inputs and N potential operations to combine hidden states, what is the size of the search space in NASNet if we have B layers? Answer: (2 × 2 × M × M × N)^B = 4^BM^2BN^B Assume M=5, N=2, B=5, we 3.2 × 10¹¹ have candidates in the design space.

Network-level Search Space

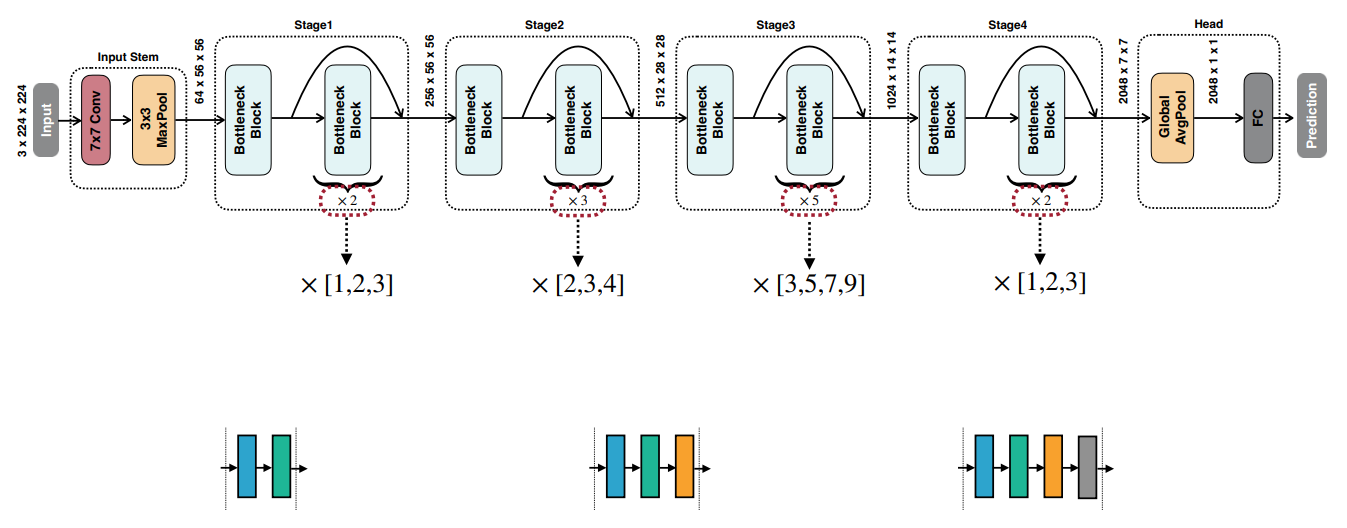
• Depth Dimension
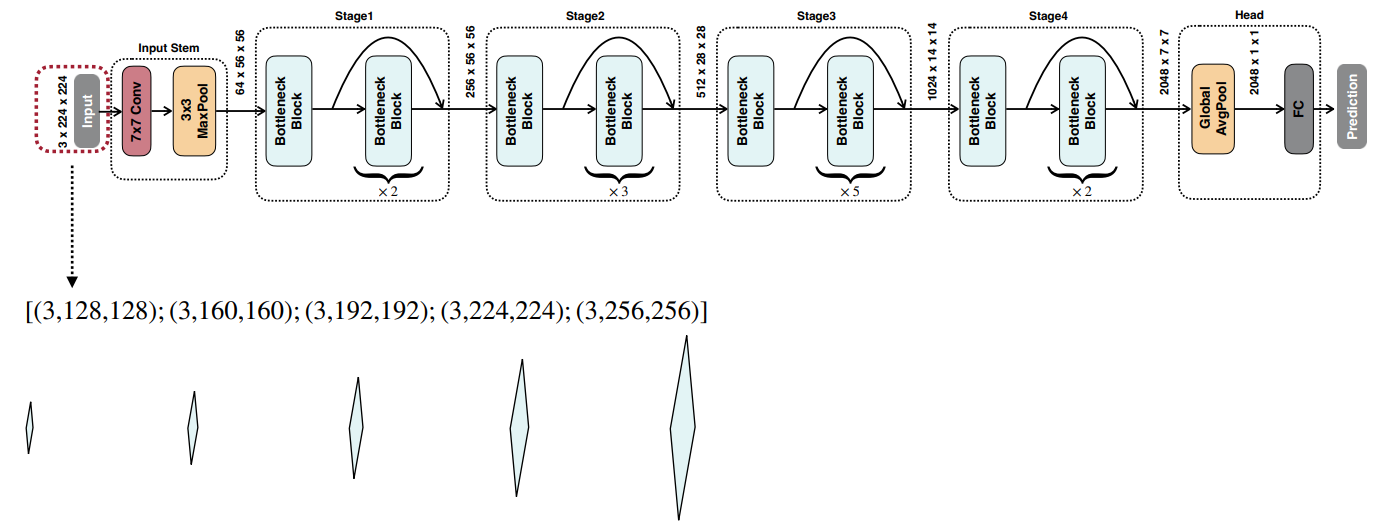
• Resolution Dimension
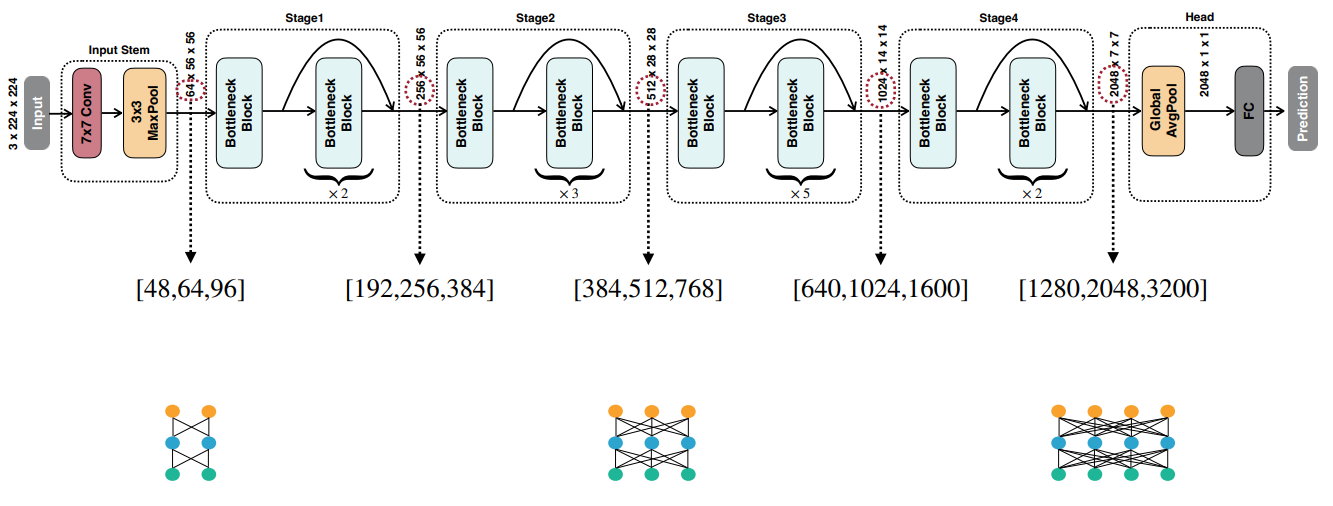
• Width Dimension
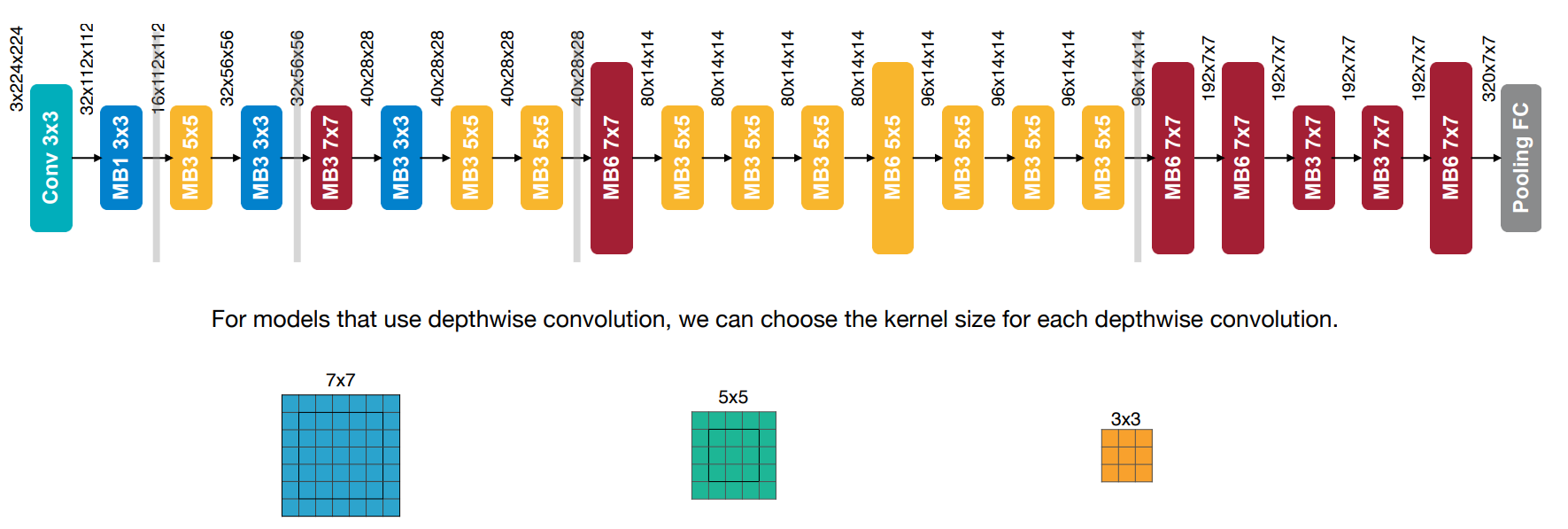
• Kernel Size Dimension
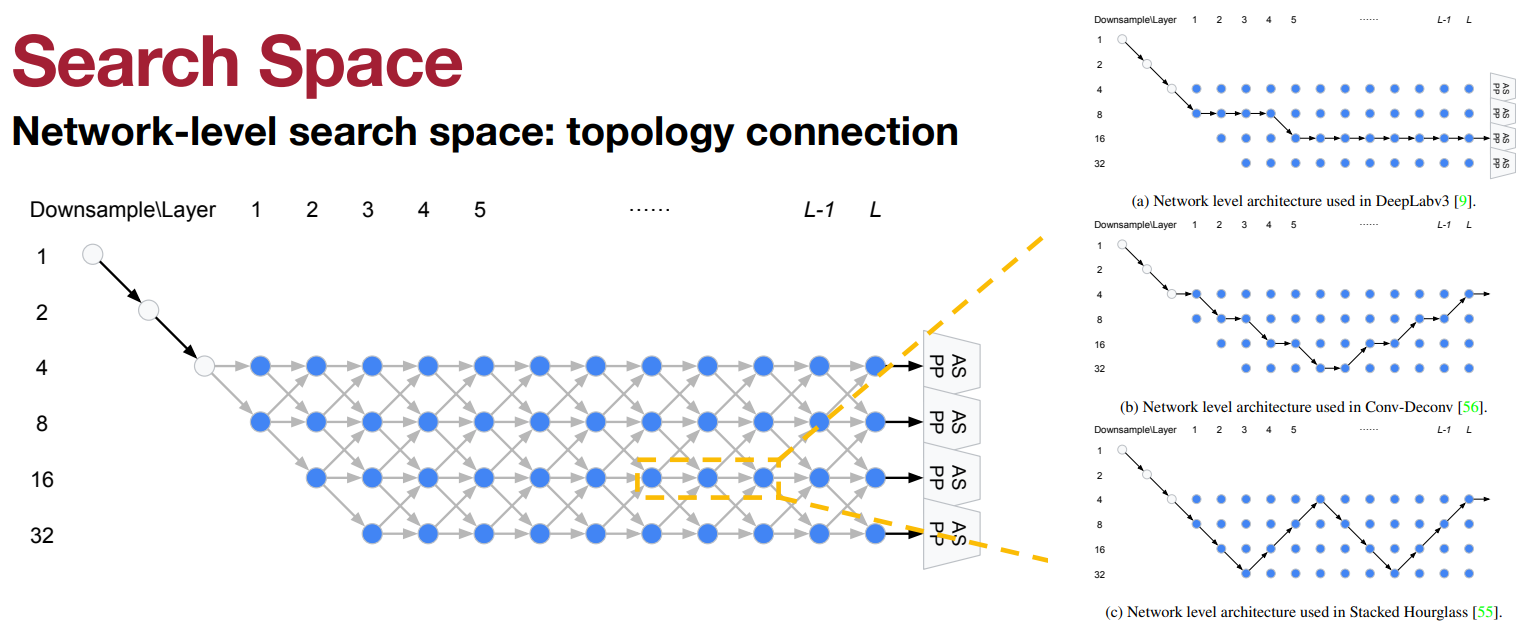
• Topology Connection
• TinyML