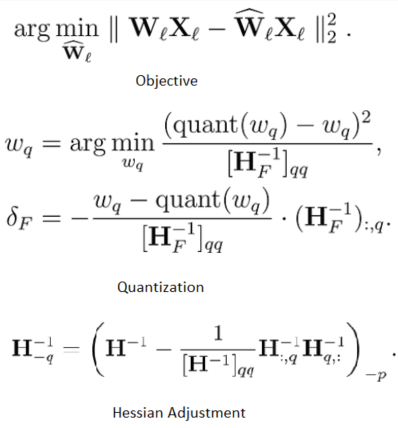• [[#Introduction

  Introduction]]

• [[#Types of Quantization

  Types of Quantization]]

  • [[#Types of Quantization#K-Means-based Weight Quantization

    K-Means-based Weight Quantization]]

  • [[#Types of Quantization#Linear Quantization

    Linear Quantization]]

    • [[#Linear Quantization#Quantization Granularities

      Quantization Granularities]]

• [[#Quantization in Training

  Quantization in Training]]

  • [[#Quantization in Training#Quantization aware Training (QAT)

    Quantization aware Training (QAT)]]

• [[#STOA Quantization Techniques

  STOA Quantization Techniques]]

  • [[#STOA Quantization Techniques#LLM.int8

    LLM.int8]]

  • [[#STOA Quantization Techniques#GPTQ

    GPTQ]]

    • [[#GPTQ#Optimal Brain Quantizer (OBQ)

      Optimal Brain Quantizer (OBQ)]]

    • [[#GPTQ#GPTQ Algorithm

      GPTQ Algorithm]]

  • [[#STOA Quantization Techniques#SmoothQuant

    SmoothQuant]]

  • [[#STOA Quantization Techniques#Activation Aware Quantization

    Activation Aware Quantization]]

  • [[#STOA Quantization Techniques#QLoRA NF4

    QLoRA NF4]]

Introduction

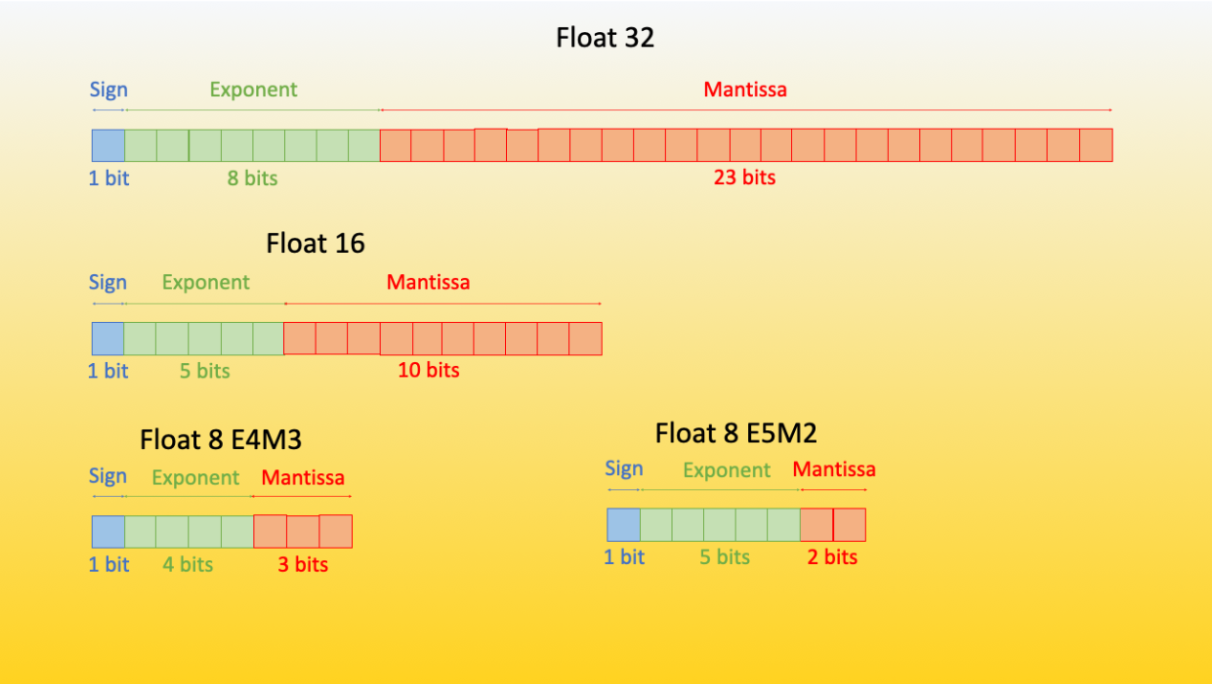
• INT8 (S1-B7) = 1 bytes (for INT there is not exponent and mantissa only bits)
• FP32 (1 sign, 8 exponent, 23 mantissa - S1-E8-M23) - requires 32 bits to store = 4x8 bits = 4 bytes
• FP16 (S1-E5-M10) = 2 bytes
• BF16 (S1-E8-M7) = 2 bytes
• FP8 (S1-E4-M3) = 1 bytes
• FP8 (S1-E5-M2) = 1 bytes
• FP4 S1E3/S1E2M1 = 0.5 bytes
• Subnormal values - E = 0
• Normal Values - E != 0

If any kernels are not implemented in fp16 try in bf16 as it is compatible with fp32 for same E

| Data Type | Size (bits) | Sign Bits | Exponent | Mantissa | Precision | Range | | ———— | ———– | ——— | ——– | ——– | ——— | —— | | Float32 | 32 | 1 | 8 | 23 | Best | ~10^38 | | Float16 | 16 | 1 | 5 | 10 | Better | ~10^4 | | BFloat16 | 16 | 1 | 8 | 7 | Good | ~10^38 | | FP8 | 8 | 1 | 4/5 | 3/2 | Avg | | | Int8 | 8 | 1 | N/A | N/A | Avg | ~2^7 |

Types of Quantization

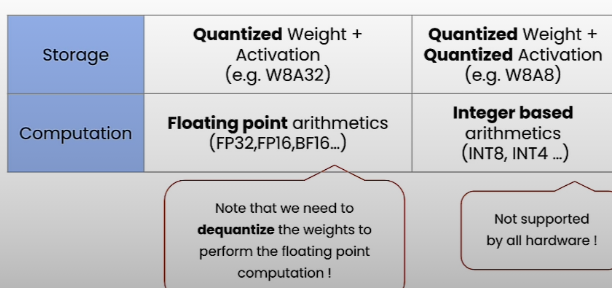
Quantization can happen in two ways:

• Activation Quantization (Calibration)
  • Range of activations varies with input
  • Use sample input, infer and calculate range of activations for linear quantization.
• Weight Quantization
  1. K-Means-based Weight Quantization
  2. Linear Quantization
     1. AWQ: Activation aware weight quantization
     2. GPTQ: GPT Quantized
     3. BNB: Bits and Bytes Quantized

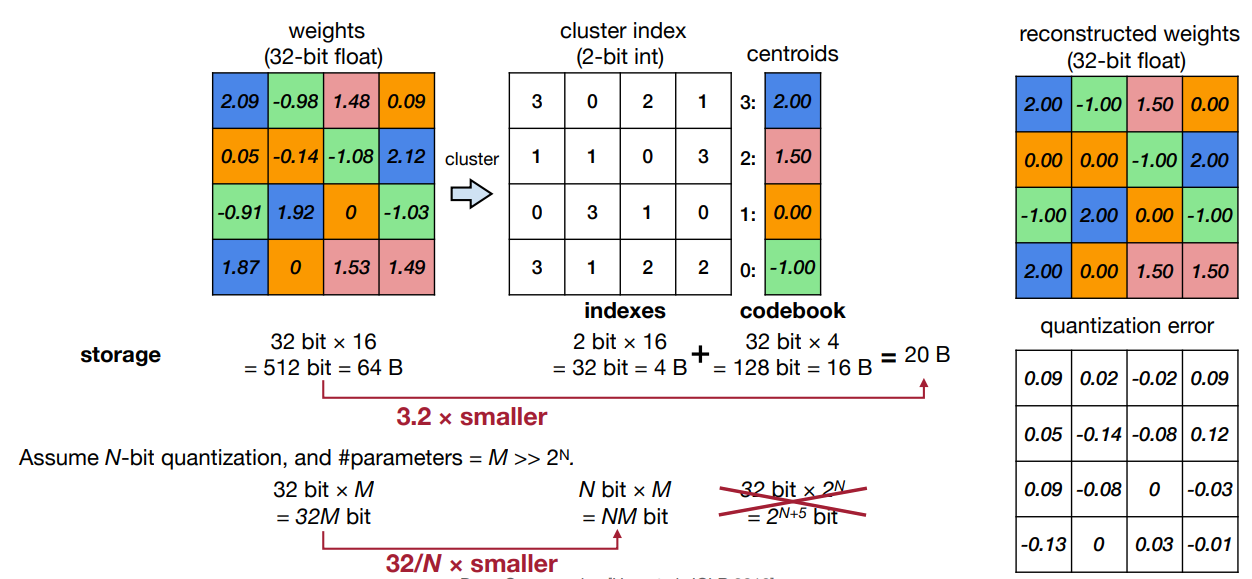
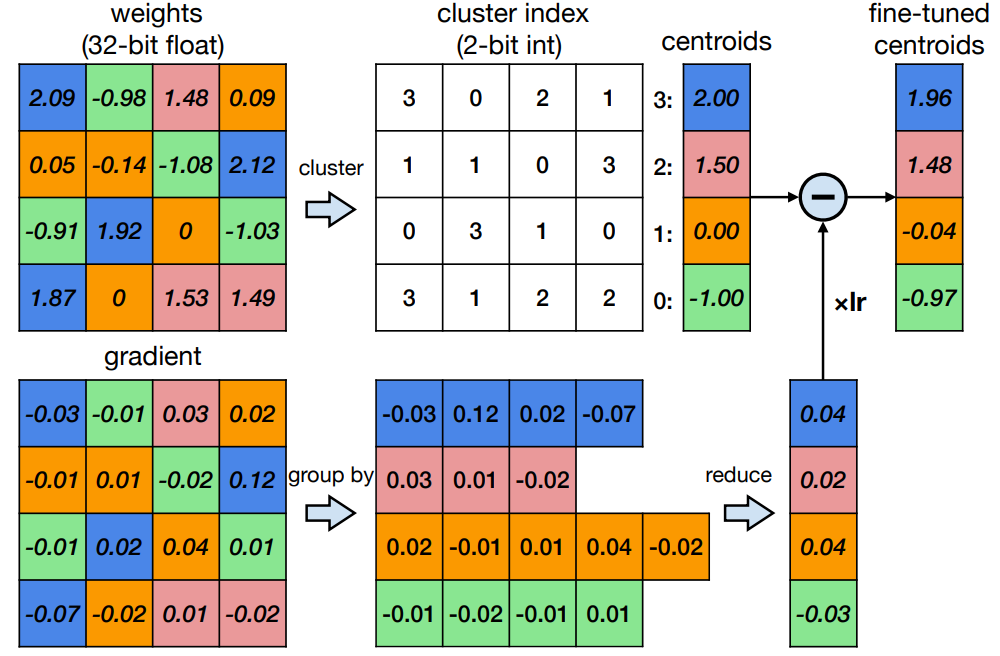
K-Means-based Weight Quantization

• Cluster weights into M clusters using any clustering algorithm.
• QAT:
  • Obtain gradients
  • Cluster gradients
  • And apply to centroids as shown below

Linear Quantization

• Symmetric
• Asymmetric

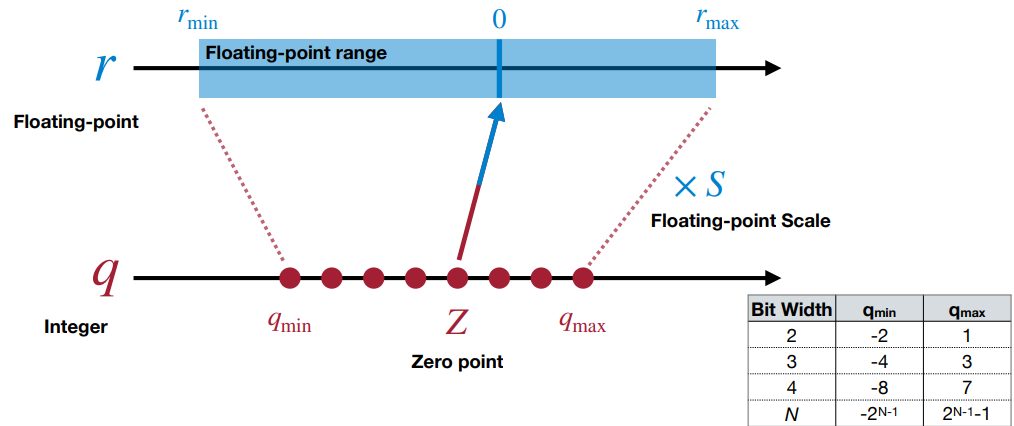
An affine mapping of integers to real numbers ==r = S(q-Z)

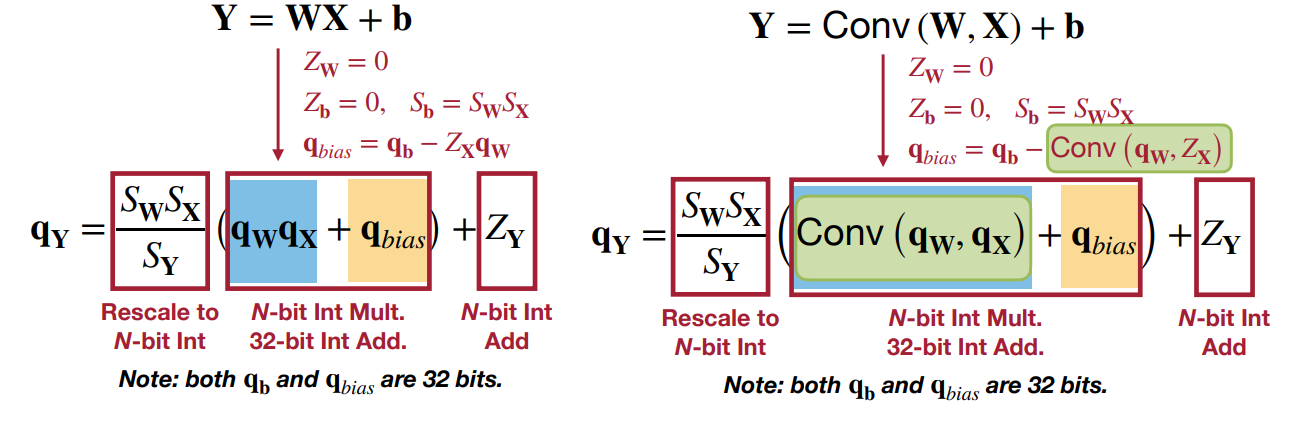
Full Connected Layer and Conv Layer:

Symmetric (SQ) vs Asymmetric (ASQ):

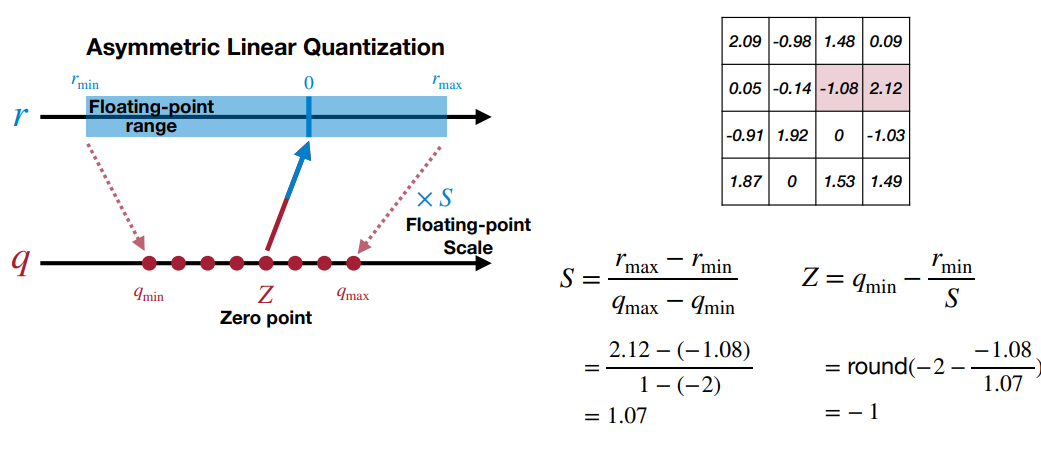
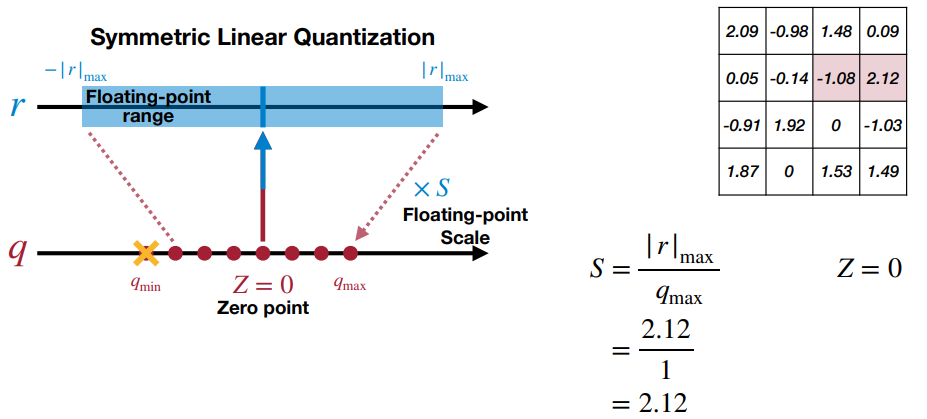
• In practice symmetric Q is used for 8 bit Q and asymmetric for 2,4 etc..
• Symmetric Q is simple but can have not so tight range which effects the Q precision and Q error.

Quantization Granularities

• Tensor - S,Z are calculated per tensor
• Channel/Vector - S,Z are calculated per channel
• Group - S,Z are calculated per group, group size are usually n=32,64,128.. elements
  • Lets say n=32 and using 4-bit SQ, resulting tensor is actually Qed to 4.5 bit
  • 4-bit (every element is stored in 4 bit) + 0.5 bit (scale in 16 bits for every 32 bits (group size n), 16/32)

Quantization in Training

• Post Training Quantization (PTQ) - All methods above
• Quantization aware Training (QAT)

Quantization aware Training (QAT)

• Quantize:
  • Quantize weight and hold both quantized (BF16) and unquantized (FP32) weights.
• Forward Pass:
  • Use Quantized version of model for inference (BF16)
• Back Prop:
  • Use original unquantized version of model weights (FP32)

STOA Quantization Techniques

• LLM.int8
• GPTQ (OBQ)
• AWQ
• QLoRA - NF4

LLM.int8

LLM.int8() seeks to complete the matrix multiplication computation in three steps:

1. From the input hidden states, extract the outliers (i.e. values that are larger than a certain threshold) by column.
2. Perform the matrix multiplication of the outliers in FP16 and the non-outliers in int8 after quantizing.
3. Dequantize the non-outlier results and add both outlier and non-outlier results together to receive the full result in FP16.

GPTQ

GPTQ is a one-shot weight quantization method based on approximate second-order information, that is both highly accurate and highly-efficient. GPTQ is inspired from OBQ.

Optimal Brain Quantizer (OBQ)

• Objective: Minimize performance degradation by quantizing weights W^{^}​ such that the outputs W^{^}X​ closely match the original outputs WX
• Quantization Process: Quantize the easiest weight first W_q, then adjust remaining non-quantized weights using $\delta$_F to compensate for the quantization error using the Hessian matrix.
• Outlier Handling: Quantize outlier weights immediately to prevent large quantization errors.
• Hessian Matrix Adjustment: For next iteration update the Hessian matrix by removing the row and column associated with the quantized weight using Gaussian elimination to avoid redundant computations.

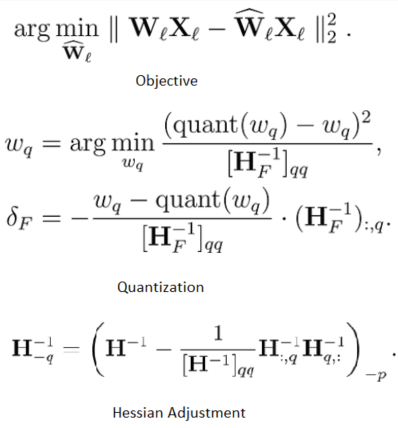
GPTQ Algorithm

• Objective: Reduce the model size while minimizing MSE same as OBQ.
• Calibration Dataset: Use a representative calibration dataset to perform inference on the quantized model, which helps in refining the quantization quality.
• Quantization Scheme: Use a hybrid quantization scheme where model weights are quantized as int4, and activations are kept in float16. During inference, weights are dynamically dequantized to float16, and actual computations are performed in float16.

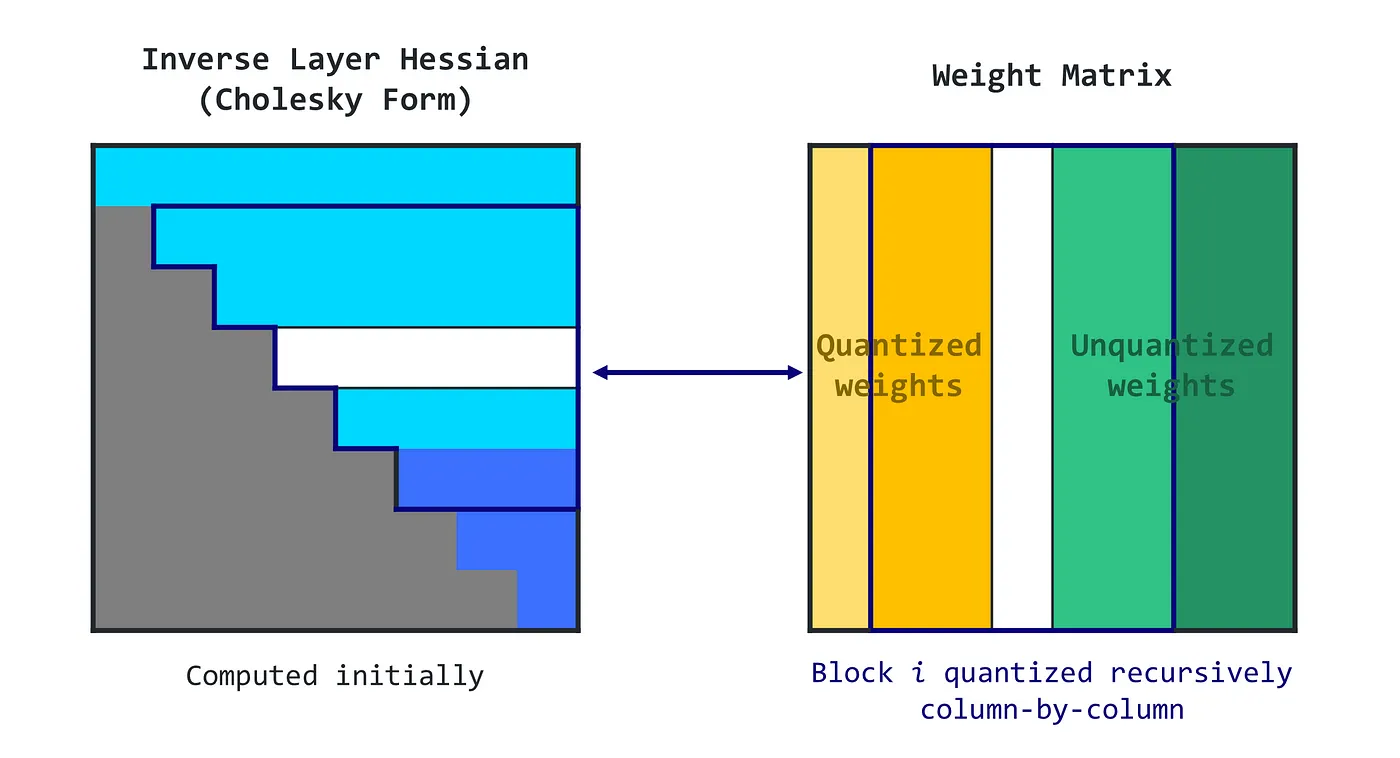
Algorithm:

1. The GPTQ algorithm begins with a Cholesky decomposition of the Hessian inverse (a matrix that helps decide how to adjust the weights)
2. It then runs in loops, handling batches of columns at a time.
3. For each column in a batch, it quantizes the weights, calculates the error, and updates the weights in the block accordingly.
4. After processing the batch, it updates all remaining weights based on the block’s errors.

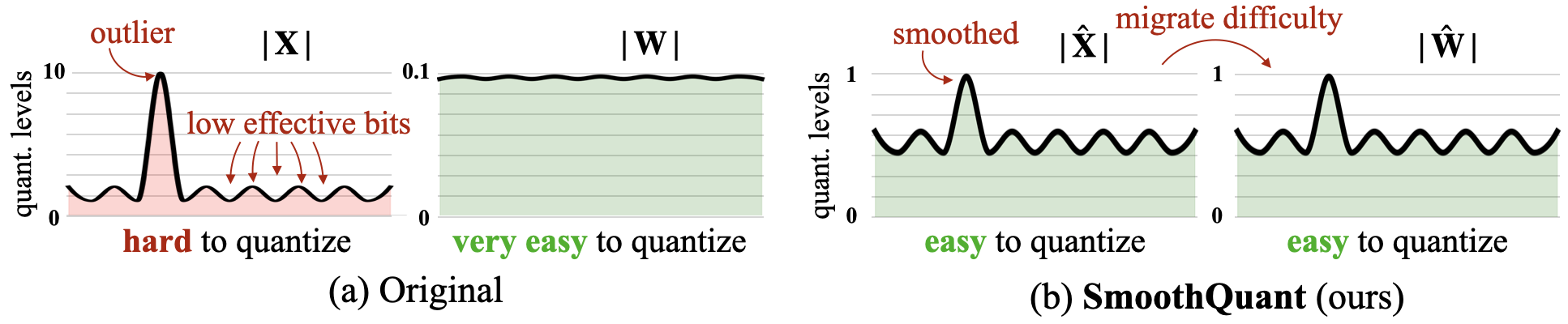
SmoothQuant

• Quantizing weights is very easy
• Quantizing activations is input dependent and is prone to more outliers
• Migrate the difficulty (outliers) from activations to weights.

Activation Aware Quantization

1. Collect Activation Statistics: During this calibration phase, a subset of the data is used to collect statistics on the activations produced by the model. This involves running the model on this data and recording the range of values and the distribution of activations.
2. Search Weight Quantization Parameters: Weights are quantized by taking the activation statistics into account (scale). Concretely, we perform a space search for quantization parameters (e.g., scales and zero points), to minimize the distortions incurred by quantization on output activations. As a result, the quantized weights can be accurately represented with fewer bits.
3. Quantize : With the quantization parameters in place, the model weights are quantized using a reduced number of bits.

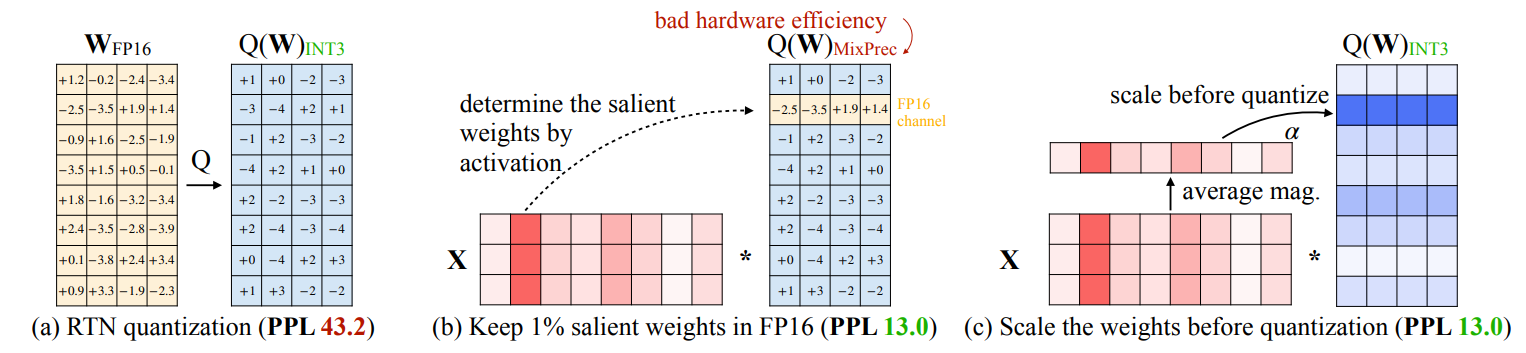
• Just keeping 1% of salient weight improves PPL(perplexity) from 43.2 to 13.0
• (c) Weights are scales based on activation statistics before Quantization.

  QLoRA NF4

• Here 4 bits are used to represent quantization level rather than actual values. So 4 bits can represent 16 levels.
• Range Selection: For NF4, the range is chosen to cover most of the weight values typically found in language models. Usually the range is [-1, 1] as layers are normalized.
• Mapping: Determine the 16 Equally/logarithmically spaced quantization levels within this range. For equal spaced example levels might be [-1, -0.8667, -0.733, …,0.6, 0.733, 0.8667, 1].
• Mapping Weight: Lets say our weight is 0.5678 find the closest NF4 value to it which is 0.6.
• Storage: Now instead of storing 0.6 like in linear mapping Q, store the level of 0.6 which is 13 as a 4-bit value.
• De-Q: Convert 13 level to 0.6 and use it, now Q err is 0.6-0.5678 = 0.0322